基本概念
如果a和d是兩個自然數,d非零,可以證明存在兩個唯一的整數 q 和 r,滿足 a = q*d + r,且0 <= r < d。其中,q 被稱為商,r 被稱為余數。
//對應代碼
int main()
{
int a = 10;
int d = 3;
printf("%d\n", a % d); //結果是1
//因為:a=10,d=3,q=3,r=1 0<=r<d(3)
//所以:a = q*d+r -> 10=3'3+1
return 0;
}
正數比較簡單,我們不談,只看負數,負數的情況還是比較復雜的,先來看看不同平臺下負數"取模"的差異
| int main() |
| { |
| int a = -10; |
| int d = 3; |
| printf("%d\n", a/d); |
| printf("%d\n", a%d); |
| } |

可以看出不同平臺下C語言"取模"和取商是沒有區別的.再看看python環境下的.
centos7默認python版本是2.7.5,故使用python 2.7.5版本測試. 也可以使用python3.7.3版本測試,結果是相同的
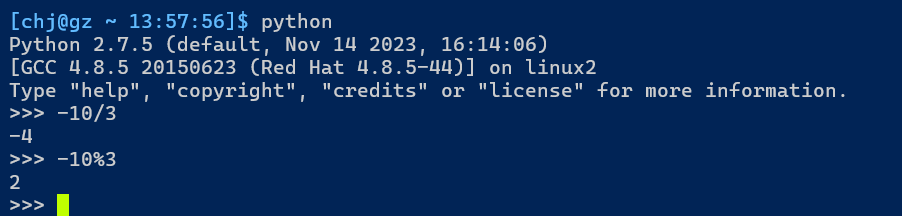
可以發現兩種語言負數求商和取余結果是不一樣的.
定義中規定,余數是要大于等于0的,而C語言卻計算出了負數.
結論:很顯然,上面關于取模的定義,并不能滿足語言上的取模運算.
因此引出了修正定義
修正定義
因為在C中,-10%3出現了負數,根據定義:滿足 a = q*d + r 且0 <= r < d,C語言中的余數,是不滿足定義的,因為,r<0了。
故,大家對取模有了一個修訂版的定義:
如果a和d是兩個自然數,d非零,可以證明存在兩個唯一的整數 q 和 r,滿足 a = q*d + r , q 為整數,且0 <= |r| < |d|。其中,q 被稱為商,r 被稱為余數。
有了這個新的定義,那么C中或者Python中的“取模”,就都能解釋了。
解釋C: -10 = (-3) ' 3 + (-1)
解釋Python:-10 = (?)' 3 + 2,其中,可以推導出來,'?'必須是-4(至于為什么,后面驗證),即-10 = (-4)' 3 + 2,才能 滿足定義。
所以,在不同語言,同一個計算表達式,負數“取模”結果是不同的。我們可以稱之為分別叫做正余數 和 負余數
是什么決定了這種現象?
具體余數r的大小,本質是取決于商的,商確定了,余數自然就能確定.
而商取決于什么? 答案是,取決于除法計算的時候,結果的取整規則.
取整規則決定商的值
C語言中取整規則默認是向0取整,python中默認取整規則是向下取整.
根據它們兩個的規則,顯然大于0的情況都是相同的,而小于0的情況是不同的,因此負數的情況下的它們的結果不相同
因為它們兩的取整規則不同,而且又必須滿足修訂版的"取模"規則,決定了它們的計算結果現象
還有一個問題,那就是既然不同語言%符號計算的值不一樣,那還是模數或余數嗎?或者說取余和取模一樣嗎?
取模和取余不一樣.
定義
取余:盡可能讓商,進行向0取整. //即零向取整方式得到的是余數
取模:盡可能讓商,向-∞方向取整. //即向下取整方式得到的是模數
//模數,在幾何向量上看,模是長度,為正值.(不考慮復數).模是正是負具體還要結合相關領域的定義.在計算機科學中,模和余很多情況是不區分的.
根據定義:
C中%運算,本質是取余數.
python中%運算,本質是取模.
再根據取整規則來看:
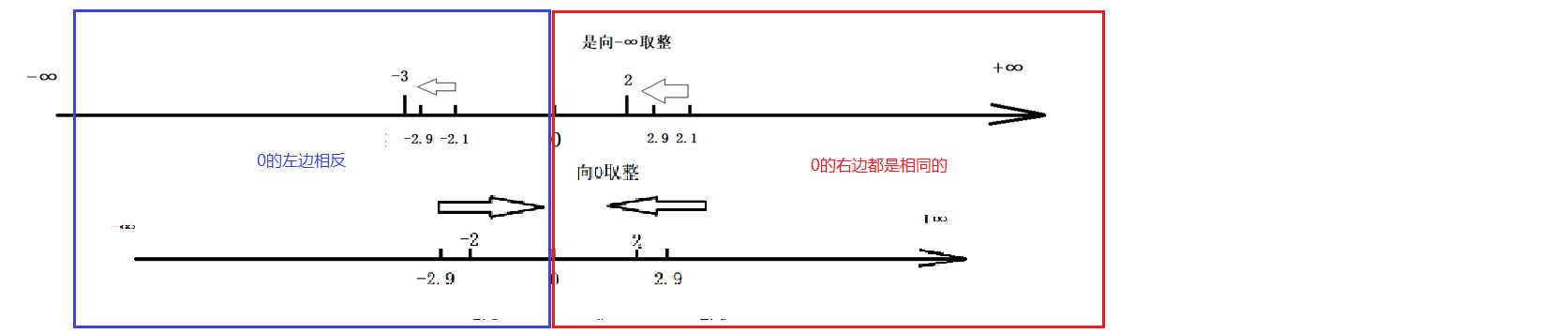
對任何一個大于0的數,對其進行0向取整和-∞取整,取整方向是一致的。故取模等價于取余
對任何一個小于0的數,對其進行0向取整和-∞取整,取整方向是相反的。故取模不等價于取余
小歸納:
同符號數據相除,得到的商,根據數學同符號相消規則,一定是正數,即大于0! 大于0取整方式就是相同的.
故,在對其商進行取整的時候,取模等價于取余。
?轉自https://www.cnblogs.com/DSCL-ing/p/18414566
該文章在 2024/12/10 8:52:52 編輯過